| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- 정답
- 도형 근사
- 2024학년도 6월 모의고사
- 2311
- 22번
- DeNA
- 고시엔 구장
- 15번
- 모두 끝까지 파이팅!
- 문제
- 2024학년도
- 수열
- 수능
- 해설
- 수학
- 240415m
- 30번
- 모의고사
- 평가원
- 한신 타이거스
- 2023학년도 대학수학능력시험
- 삼도극
- 미적분
- 2025학년도 수능
- 수학2
- 수학1
- 9모
- 풀이
- 공통
- 식 근사
- Today
- Total
JS
2025학년도 대학수학능력시험 공통 20번 해설, 문제, 정답, 풀이 [251120m] 본문
아마 이 글을 읽는 사람은 2026학년도 수능, 또는 그 이후의 수능을 준비하는 학생이 아닐까 싶다. 기출문제를 다시 풀어본다는 것은 매우 좋은 것이라 생각한다. 출제자가 어떤 스타일로 내는지, 어떤 형태에서 어떤 방식으로 풀이를 유도하는지, 문제를 멀리서도 바라보고 가까이 바라보기도 하면서 한 문제의 다양한 면모를 찾아내는 것이 중요하다.
여유를 갖고 한 문제를 끝까지 뜯어내는 것도, 혼자서 이미지 트레이닝으로 시간에 쫓겨 수능 시험을 보고있다는 마인드로 급박하게 풀어내는 것도 모두 좋은 방법이다
필자는 이 글을 통해 수험생들에게 또 다른 하나의 시각을 부여하고, 이런 방법으로도 풀 수 있겠구나 대안을 제시해주고싶어 이 글을 작성하였다.
처음 풀 때 쉽지만은 않다고 느낀 문제이다. 만약 시험장에서 봤다면 복잡하게 생긴 숫자에 마냥 쉽게 보이지 않는 풀이 방법까지, 평정심을 잘 유지하지 못했다면 시험장에서는 어려웠을 수 있는 문제라고 생각한다. 하지만, 계산이 복잡한 문제는 아니기에 방법만 찾았다면 쉽게 풀었을 것이다.
2025학년도 수능 수학 문제지 다운로드(한국교육과정평가원)
답지(해설X) 다운로드(한국교육과정평가원)
문제
![20. 곡선 y=(1/5)^(x-3) 과 직선 y=x 가 만나는 점의 x 좌표를 k 라 하자. 실수 전체의 집합에서 정의된 함수 f(x) 가 다음 조건을 만족시킨다.
<조건>
x>k 인 모든 실수 x 에 대하여
f(x)=(1/5)^(x-3) 이고 f(f(x))=3x 이다.
f(1/(k^3 * 5^{3k}) 의 값을 구하시오. [4점]](https://blog.kakaocdn.net/dna/b18QJL/btsOZx8jTU1/AAAAAAAAAAAAAAAAAAAAAIQcSoOLPgSV9_Y4npddCKlitRrHTaD3rmxkMv7FdOVO/img.png?credential=yqXZFxpELC7KVnFOS48ylbz2pIh7yKj8&expires=1753973999&allow_ip=&allow_referer=&signature=f1MPb5bI2fEw7LFE%2B3N8GqOA8iM%3D)
20. 곡선 $\displaystyle y=\left(\frac{1}{5}\right)^{x-3}$ 과 직선 $y=x$ 가 만나는 점의 $x$ 좌표를 $k$ 라 하자. 실수 전체의 집합에서 정의된 함수 $f(x)$ 가 다음 조건을 만족시킨다.
| <조건> $x>k$ 인 모든 실수 $x$ 에 대하여 $f(x)=\left(\frac{1}{5}\right)^{x-3}$ 이고 $f(f(x))=3 x$ 이다. |
$\displaystyle f\left(\frac{1}{k^3 \times 5^{3 k}}\right)$ 의 값을 구하시오. [4점]
정답
정답: 36
해설
일단 그래프인 $\displaystyle y=\left(\frac{1}{5}\right)^{x-3}$ 과 $y=x$를 먼저 그려서 $k$값과 문제 상황을 이해하는데 초점을 두는것이 일반적이겠다.
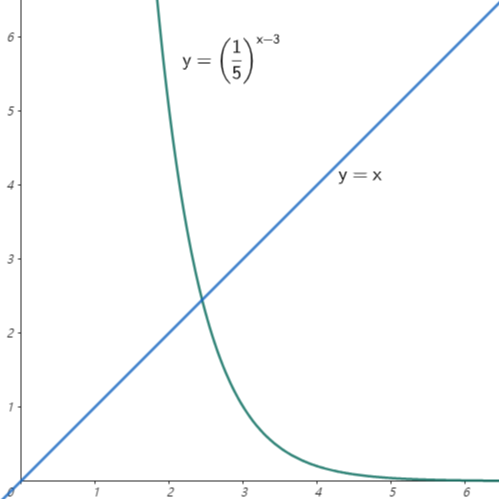
그래프를 그리면 $k$값의 범위와 $f(x)$의 형태를 추측할 수 있다.
$k$값의 범위 : $2<k<3$
$f(x)$는 $x=k$를 기점으로 오른쪽의 부분
오케이. 그림으로 얻을 수 있는 힌트는 여기까지인 것 같으므로, $k$값에 대한 식을 만들어보자.
$\displaystyle\left(\frac15\right)^{k-3}=k$라고 식을 세우고 값을 정리하면 $k\cdot5^k=5^3$임을 구할 수 있다.
어? 이 모양은 어디에서 많이 봤는데?
그렇다. 정답에서 요구하는 값인 $\displaystyle{f}\left(\frac{1}{k^3\times5^{3k}}\right)$에서 보던 모양이다.
$\displaystyle\frac{1}{k^3\times5^{3k}}$은 $\displaystyle\left(\frac{1}{k\cdot5^k}\right)^3$으로 볼 수 있고, 위에서구한 $k\cdot5^k=5^3$을 사용하면 결국 $\displaystyle{f}\left(\frac{1}{5^9}\right)$값을 구하란 말임을 알 수 있다.
우리가 아직까지 상자속 조건을 사용하지 않았다.
그렇다. 상자속 조건을 사용하면 답에 더 가까이 갈 수 있겠구나!
그래서 사용하려고 들여다보니... 조금 복잡해보이는데? 합성도 되어있고 x값의 범위도 제한되어있고
하지만, 여기에서 당황하면 안된다. 천천히 끝까지 읽다보면 문제 풀이의 실마리를 잡을 수 있을 것이다.
아무래도 $f(f(x))=3x$가 제일 신경쓰이고 문제 풀이에 핵심적인 역할을 갖고 있다는 느낌을 받는다.
이 조건을 잘 써야할텐데... $\displaystyle{x}=\frac{1}{5^9}$를 바로 넣기엔 범위가 맞지 않는데, 다른 방법을 찾다보면
속에 있는 $f(x)$의 $x$에 적당한 값을 넣어 얻은 값이 $\displaystyle\frac{1}{5^9}$이면 된다는 생각이 날 것이다. 그 적당한 값은 $12$이고, 결국 구한 값은 $36$.
$\therefore \text{답}=36$
문제 검색 하는 법
문제 검색 하는 법 : [학년도/시행월/문제번호/과목명]
과목명 : [m - 수학 1ᐧ수학 2ᐧ미적분]
ex) 24학년도 6월 모의고사 미적분 30번 풀이의 경우 "240630m"(으)로 검색
혹시 오류가 있다면 언제든 지적 부탁드립니다! 감사합니다!
'모의고사·수능 > 수학 2025학년도' 카테고리의 다른 글
| 2025학년도 대학수학능력시험 미적분 27번 해설, 문제, 정답, 풀이 [251127m] (0) | 2025.04.13 |
|---|

