JS
2024학년도 6월 미적분 29번 엄청 쉬운 풀이 / 틀렸으면 들어와서 확인하기! [240622m] 본문
오답률
2024학년도 6월 모의고사 수학 미적분
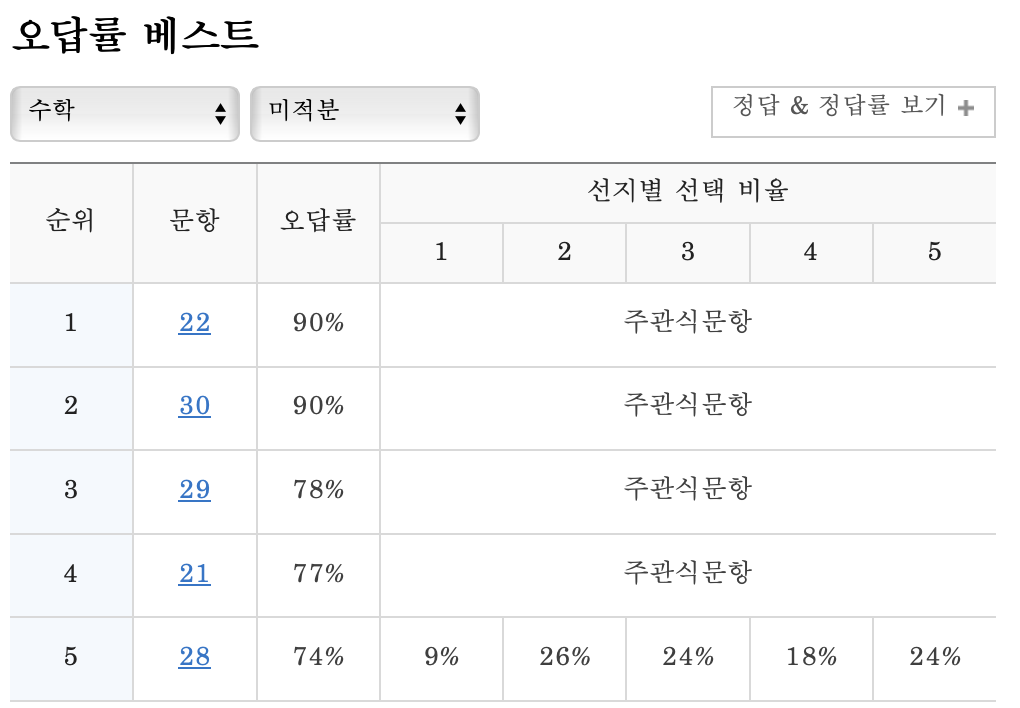

메가스터디와 EBSi 오답률을 찾아보면 많은 학생들이 29번, 22번, 30번을 포함한 기존 준킬러-킬러 문항대에서 어려움을 느낀 것을 알 수 있다. 개인적으로는 미적분 28번이 상당히 어려웠다고 생각했는데, 오답률 베스트 5에는 끼지도 못 한점이 의외이다.
이번 게시글에서 풀이할 29번은 조금만 센스 있게 풀이하면 간단히 풀이할 수 있다. 이번 문제를 통해 미분, 식 조작 방법을 마스터 하면 될 듯 하다. 또, 문제에서 조건을 두 접선이 직각이라고 주어줬지만, 충분히 다른 각도를 주어 계산하게 할 수 있을 것이다. 물론, 이렇게 문제를 출제한다면 조금 쉽게, 또 문항 번호도 앞에 두겠지만.
평가원은 6월, 9월에 출제 했던 미분/적분 문제에서 비슷한 개념을 차용해 적분/미분 문제를 만드는 경향이 있다. 9월 모의고사 문제를 봐야 알겠지만, 이번 수능 28, 29, 30번에 이와 비슷한 적분 문제가 출제될 가능성을 충분히 염두해 두고 공부해야 한다.
(왼쪽 자료 출처 : 메가스터디 https://www.megastudy.net/Entinfo/2024_jungsi/exam/Exam_main.asp?seq=311&SubMainType=I&mOne=ipsi&mTwo=435)
(오른쪽 자료 출처 : Ebsi https://www.ebsi.co.kr/ebs/xip/xipa/retrievePastGrdCutWrongAnswerRate.ebs?tab=1)
문제

세 실수 $a,\,b,\,k$에 대하여 두 점 $A(a,a+k)$, $B(b,b+k)$가 곡선 $C:x^2-2xy+2y^2=15$ 위에 있다. 곡선 $C$ 위의 점 $A$ 에서의 접선과 곡선 $C$ 위의 점 $B$에서의 접선이 서로 수직일 때, $k^2$ 의 값을 구하시오. (단, $a+2k\neq0,\,b+2k\neq0$) [4점]
정답
( 단답형 ) 5
해설

우선 곡선 $C$를 $y$에 대해 미분하면 $\displaystyle2x-2y-2x\frac{dy}{dx}+4y\frac{dy}{dx}=0$이다.
$\displaystyle\frac{dy}{dx}=\frac{x-y}{x-2y}\,(\text{단, }x-2y\neq0)$

두 점 $A$, $B$에서의 접선의 기울기는 각각 $\displaystyle\frac{k}{2k+a}$, $\displaystyle\frac{k}{2k+b}$이다. (문제에서 $a+2k\neq0,\,b+2k\neq0$ 조건을 제공함)

문제에서 두 접선이 수직이라고 했으니 기울기의 곱은 $-1$, 즉 $\displaystyle\frac{k}{2k+a}\frac{k}{2k+b}=-1$이다.
정리하면 $3k^2+2k(a+b)+ab=0$

또, 우리는 곡선 위의 점의 좌표를 아니깐 대입해서 값을 얻을 수 있다.
$C:(x-y)^2+y^2=15$
각각 두 점을 대입하면
$k^2+(a+k)^2=15,\,k^2+(b+k)^2=15$를 얻을 수 있고,
두 식을 서로 빼면 $(a+k)^2=(b+k)^2$를 구할 수 있다.
즉, $a+k=b+k$, 또는 $a+k=-(b+k)$
그런데, 첫번째의 경우에는 $a=b$, 곡선의 같은 점에서의 기울기가 서로 수직일 수 없으므로 모순.
그러므로 $a+b=-2k$이다.
위에서 구한 $3k^2+2k(a+b)+ab=0$에 $a+b=-2k$를 넣어 계산하면 $k^2=-ab$를 얻을 수 있다.
이제 거의 다 왔다.
-마지막 계산 방법 1-

위에서 구한 $15=k^2+(a+k)^2$에서 k를 없애는 방향으로 식을 조작하면
$\begin{align}15&=k^2+a^2+a\cdot 2k+k^2\\
&=-ab+a^2-a(a+b)-ab\\
&=-3ab\end{align}$
$ab=-5$이다.
$k^2=-ab$였으므로, $k^2=5$
-마지막 계산 방법 2-

$a+b=-2k$, $ab=-k^2$이었다.
$a$와 $b$를 이차방정식의 두 근이라고, 또 위의 두 식은 근과 계수의 관계를 알려준 것이라고 생각하면 $a$와 $b$를 $k$로 표현할 수 있다.
두 근의 평균은 $-k$이고, 각각 같은 거리 미지수 $p$만큼 떨어져 있다.
두 근의 곱이 $-k^2$이었으므로
$(-k+p)(-k-p)=-k^2$
$p=\pm\sqrt{2k}$
$a$와 $b$의 좌표는 $-k\pm\sqrt{2k}$이다.
이렇게 구한 좌표를 다시 곡선의 방정식에 대입해주면
$k^2+(\sqrt{2k})^2=15$, $k^2=5$가 나온다.
학습에 도움이 되었으면 하고, 앞으로 검색할 때 여기에서 우선적으로 찾으면 편하게끔 하려고 한다. 혹시 풀이가 필요한 수학문제, 국어문제, 물리문제가 있다면 무슨 모의고사 몇 번 문제인지 아래 폼으로 알려주면 우선적으로 추가하겠다.
파일을 포함한 질문은 여기로 >> https://forms.gle/mMjHoqgRuY1dUtyy9
문제 검색 하는 법
문제 검색 하는 법 : [학년도/시행월/문제번호/과목명]
과목명 : [m - 수학 1ᐧ수학 2ᐧ미적분, k - 독서ᐧ문학ᐧ언어와 매체, p - 물리학 1]
ex) 24학년도 6월 모의고사 미적분 30번 풀이의 경우 "240630m"(으)로 검색
혹시 오류가 있다면 언제든 지적 부탁드립니다! 감사합니다!
'모의고사·수능 > 수학 2024학년도' 카테고리의 다른 글
| 2024학년도 9월 모의고사 미적분 30번 해설, 문제, 정답, 풀이 [240930m] (5) | 2023.09.07 |
|---|---|
| 2024학년도(2023년 시행) 4월(5월) 모의고사 공통 15번 해설, 문제, 정답, 풀이 [240415m] (0) | 2023.06.27 |
| 2024학년도(2023년 시행) 6월 수학 공통 22번 (오답률 1위) 엄청 쉬운 풀이, 문제, 정답, 해설, 정답률 [240622m] (0) | 2023.06.25 |
| 2024학년도(2023년 시행) 6월 모의고사 공통 12번 해설, 문제, 정답, 풀이 [240612m] (0) | 2023.06.25 |
| 2024학년도(2023년 시행) 6월 모의고사 공통 13번 해설, 문제, 정답, 풀이 [240613m] (0) | 2023.06.24 |




