JS
2024학년도(2023년 시행) 6월 모의고사 공통 12번 해설, 문제, 정답, 풀이 [240612m] 본문
2024학년도(2023년 시행) 6월 모의고사 공통 12번 해설, 문제, 정답, 풀이 [240612m]
seook 2023. 6. 25. 00:00
필자의 부족한 평가
어려운 문항의 번호대는 아니지만, 내가 풀이한 방법이 일반적이지 않다고 생각해 이렇게 풀이를 올리게 되었다.
문제

$a_2=-4$이고 공차가 $0$이 아닌 등차수열 $\{a_n\}$에 대하여 수열 $\{b_n\}$을 $b_n=a_n+a_{n+1}\,(n\geq 1)$이라 하고, 두 집합 $A,\,B$를
$$A=\{a_1,a_2,a_3,a_4,a_5\}\;B=\{b_1,b_2,b_3,b_4,b_5\}$$
라 하자. $n(A\cap B)=3$이 되도록 하는 모든 수열 $\{a_n\}$에 대하여 $a_{20}$의 값의 합은? [4점]

정답
( 객관식 ) 5번 : 46
해설
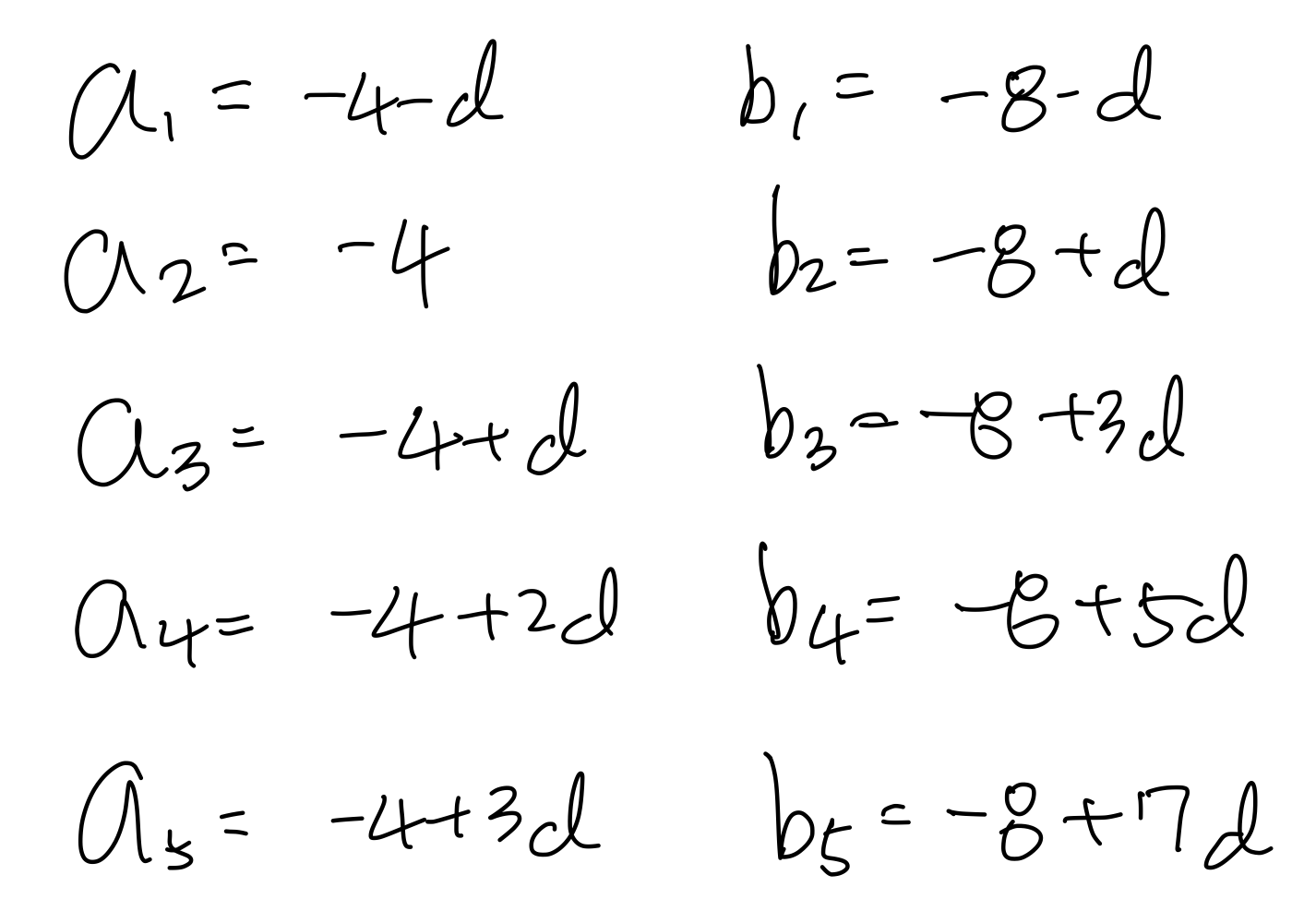
$A$와 $B$를 표현하면
| $A$ | $B$ |
| $a_1=-4-d$ | $b_1=-8-d$ |
| $a_2=-4$ | $b_2=-8$ |
| $a_3=-4+d$ | $b_3=-8+d$ |
| $a_4=-4+2d$ | $b_4=-8+2d$ |
| $a_5=-4+3d$ | $b_5=-8+3d$ |

$n(A\cap B)=3$이라는 것은 어떤 $a_n$과 어떤 $b_i$이 서로 같다, 즉 둘이 빼면 0의 값을 갖는다라고 생각할 수 있다. 표를 그려 아래처럼 문제를 해결해보자.
| $a_n-b_i$ | $a_1$ | $a_2$ | $a_3$ | $a_4$ | $a_5$ |
| $b_1$ | $4$ | $4+d$ | $4+2d$ | $4+3d$ | $4+4d$ |
| $b_2$ | $4-2d$ | $4-d$ | $4$ | $4+d$ | $4+2d$ |
| $b_3$ | $4-4d$ | $4-3d$ | $4-2d$ | $4-d$ | $4$ |
| $b_4$ | $4-6d$ | $4-5d$ | $4-4d$ | $4-3d$ | $4-2d$ |
| $b_5$ | $4-8d$ | $4-7d$ | $4-6d$ | $4-5d$ | $4-4d$ |

$a_n-b_i$가 같은 값을 갖는, 또 그 값이 0인 것을 표에서 구하면 색칠 된 것처럼 $4-2d$ 또는 $4-4d$인 것을 알 수 있다.
즉 $d=2\text{또는}1$
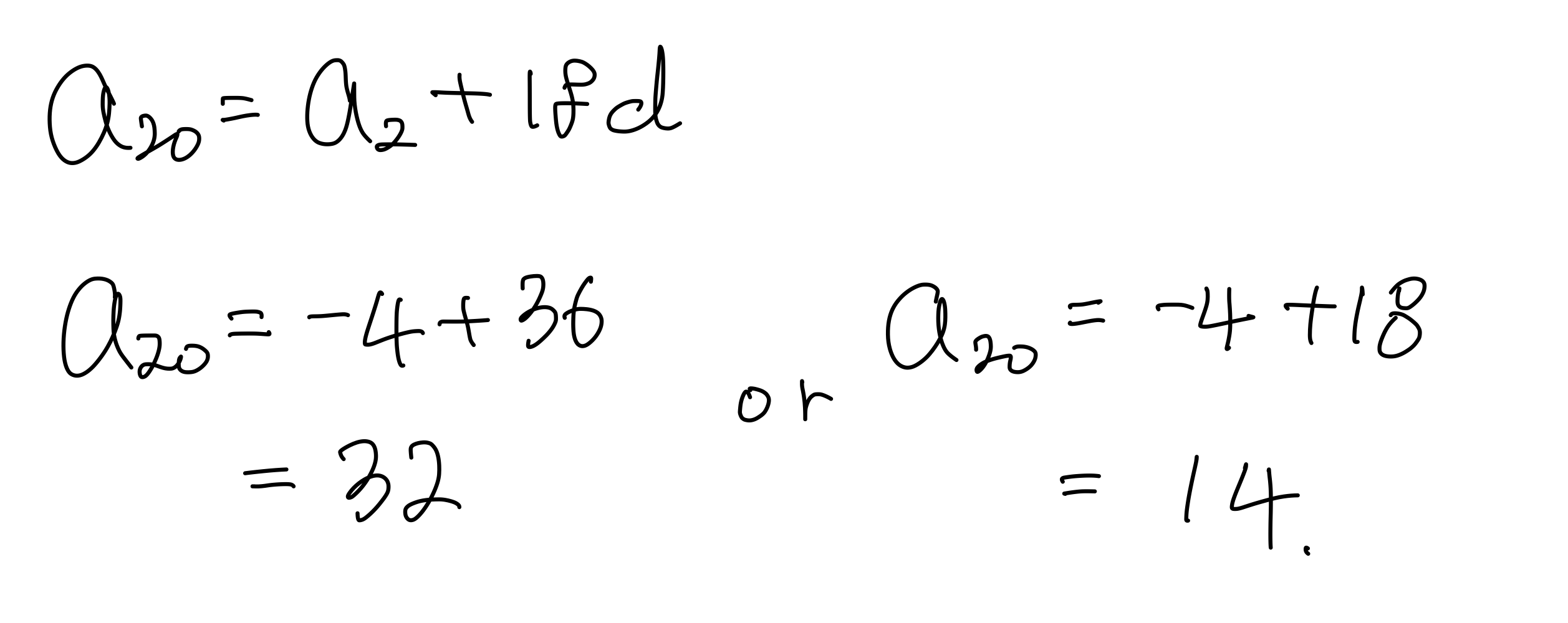
$a_{20}=a_2+18d$ 이다. $a_{20}$의 값을 구하면
$\begin{align}a_{20}&=-4+36\\
&=32\end{align}$
또는
$\begin{align}a_{20}&=-4+18\\
&=14\end{align}$

이므로, 모든 $a_{20}$의 값의 합은 $32+14=46$
$\therefore 46$이다.
학습에 도움이 되었으면 하고, 앞으로 검색할 때 여기에서 우선적으로 찾으면 편하게끔 하려고 한다. 혹시 풀이가 필요한 수학문제, 국어문제, 물리문제가 있다면 무슨 모의고사 몇 번 문제인지 아래 폼으로 알려주면 우선적으로 추가하겠다.
파일을 포함한 질문은 여기로 >> https://forms.gle/mMjHoqgRuY1dUtyy9
문제 검색 하는 법
문제 검색 하는 법 : [학년도/시행월/문제번호/과목명]
과목명 : [m - 수학 1ᐧ수학 2ᐧ미적분, k - 독서ᐧ문학ᐧ언어와 매체, p - 물리학 1]
ex) 24학년도 6월 모의고사 미적분 30번 풀이의 경우 "240630m"(으)로 검색
혹시 오류가 있다면 언제든 지적 부탁드립니다! 감사합니다!
'모의고사·수능 > 수학 2024학년도' 카테고리의 다른 글
| 2024학년도 6월 미적분 29번 엄청 쉬운 풀이 / 틀렸으면 들어와서 확인하기! [240622m] (1) | 2023.06.27 |
|---|---|
| 2024학년도(2023년 시행) 6월 수학 공통 22번 (오답률 1위) 엄청 쉬운 풀이, 문제, 정답, 해설, 정답률 [240622m] (0) | 2023.06.25 |
| 2024학년도(2023년 시행) 6월 모의고사 공통 13번 해설, 문제, 정답, 풀이 [240613m] (0) | 2023.06.24 |
| 2024학년도(2023년 시행) 4월(5월) 모의고사 공통 15번 해설, 문제, 정답, 풀이 [240415m] (1) | 2023.05.17 |
| 2024학년도(2023년 시행) 4월(5월) 수학 미적분 29번 해설, 문제, 정답, 풀이 [240429m] (0) | 2023.05.10 |




