JS
2024학년도(2023년 시행) 3월 수학 공통 22번 (오답률 1위)해설, 문제, 정답, 풀이, 정답률 [240322m] 본문
2024학년도(2023년 시행) 3월 수학 공통 22번 (오답률 1위)해설, 문제, 정답, 풀이, 정답률 [240322m]
seook 2023. 4. 30. 14:26해설은 조금 밑으로 스크롤(서론이 길음)
교육청 모의고사는 2023학년도를 기준으로 시행되지만, 평가원 모의고사와 수능은 졸업 연도를 기준으로 2024학년도로 표기된다. 이는 집중하는 시점의 차이이다. 필자는 미래가 현재보다 더 중요하다는 견해를 가지고 있으며, 다른 학습 자료와 일관성을 유지하기 위해 공식 명칭이 2023학년도 3월 모의고사라 할지라도 실제로는 2024학년도 3월 모의고사로 표기할 것이다.
이 모의고사를 친 고등학교 3학년 현역 학생들은 입학할 때부터 코로나 19로 인해 학교생활을 제대로 못한 비운(?)의 아이들이다. 나중에 고등학생 때를 뒤돌아 보면 어떤 회상을 할지 궁금한데,,, 예상하기로는 게임한 기억, 독서실에서 공부한 기억 또는 친구들과 소소하게 놀았던 기억이 지배적일 것 같다. "고등학생"으로서의 추억이 아닌, 단지 "학생"으로서의 추억. (물론 이게 좋고 저게 나쁘다는 뜻은 아니다)

3월 모의고사 오답률(정답률)이다. 미적분 기준 정답률 3.4%를 보여주며 오답률 1위를 당당히 차지하고 있는 모습을 볼 수 있다. 1위부터 6위까지 오답률은 국룰 6인방 (20, 21, 22, 28, 29, 30)이 차지하고 있다. 아직 미적분 진도를 다 나가지 않은 3월 모의고사인만큼 미적분 문제보다는 공통 문제에 더욱 힘을 주어 복습하면 좋을 듯하다.
필자의 부족한 평가
우선 고등학교 3학년이 되고 시행한 첫 모의고사라는 점에서 "상징적"인 시험이다. 시험 결과가 어떻든 여기에서 몇 문제난 틀렸던 상관없이 수능날까지 꾸준히 노력하면 원하는 성적에 더더욱 근접할 것은 틀림없다.
2024학년도 3월 모의고사(2023년 시행) 수학 공통 22번은 솔직히 말해 굉장히 "흔한" 문제다. 물론 이 문제를 틀린 대다수의 현역 학생들은 내신과 병행하느라 정시 공부를 할 시간이 부족해서 그런 것임을 충분히 이해한다. 하지만, 이 문제를 접근마저 못했다면 정말 분발해야 할 것이다.
수능을 보기 전까지는 답을 맞혔는지 만큼 중요한 것이 있다. 바로 얼마나 효율적으로 스마트하게 문제를 접근해 나가고 풀이했는지이다. 문제를 틀리고 맞고에 집중하기보다 어떻게 풀었는지 생소한 표현이 나왔을 때 예시를 들며 상황을 이해할 수 있는지 짚고 넘어가는 게 좋을 것이다.
이 문제를 풀고 2023학년도 대학수학능력시험 수학 공통 22번도 상황을 이해하는 연습을 추가적으로 하면 좋을 것이다. 바로 아래에 수능 22번 문제 다운로드 링크와 해설 링크를 적어놓을 테니, 자습하는 학생들은 참고하면 좋겠다.
2024학년도 3월 모의고사 수학 22번, 2023학년도 대수능 수학 22번 문제 합본 다운로드
2023.04.30 - [모의고사·수능/수학 2023학년도] - 2023학년도 11월 (대수능) 수학 공통 22번 해설, 문제, 정답, 풀이 [231122m]
2023학년도 11월 (대수능) 수학 공통 22번 해설, 문제, 정답, 풀이 [231122m]
필자의 부족한 평가 질린다. 하지만 질리도록 풀어도 새롭다. (뭐 이런 모순적인) 이전에 기출문제에서 자주 본 형식의 문제이다. (가) 조건에 주어진 식을 이항하고 나누어 기울기로 해석하는,
seook.tistory.com
문제


아래 글이 위 사진처럼 자연스럽지 않다면 >> https://seook.tistory.com/20
최고차항의 계수가 $1$인 사차함수 $f(x)$가 있다. 실수 $t$에 대하여 함수 $g(x)$를 $g(x)=\lvert f(x)-t \rvert$라 할 때, $\displaystyle\lim_{x\to k}\frac {g(x)-g(k)}{\lvert x-k \rvert}$의 값이 존재하는 서로 다른 실수 $k$의 개수를 $h(t)$라 하자.
함수 $h(t)$는 다음 조건을 만족시킨다.
(가) $\displaystyle\lim_{t\to 4+} h(t)=5$
(나) 함수 $h(t)$는 $t=-60$과 $t=4$에서만 불연속이다.
$f(x)=4$이고, $f^\prime(2)>0$일 때, $f(4)+h(4)$의 값을 구하시오.
정답
(주관식) : $729$
해설
5단계의 도약을 거쳐 답을 구할 것이다. 천천히 따라가보자.
1. 문제의 전반적인 상황을 이해해보자.
$g(x)=\lvert f(x)-5 \rvert$는 $f(x)$와 $y=t$를 긋고, $y=t$아래로 내려가는 곡선은 접어서 위로 올려주라는.. 매우 흔한 표현이니 바로 넘어가겠다. (만약 이게 이해가 안 되면 이 문제를 도전하고 있으면 안 된다.)

$\displaystyle\lim_{x\to k}\frac {g(x)-g(k)}{\lvert x-k \rvert}$의 값이 존재한다는데, 분모에 절댓값이 들어가 있으니 우극한과 좌극한으로 쪼개어 절댓값을 벗겨보자.
$\displaystyle\lim_{x\to k+}\frac {g(x)-g(k)}{\lvert x-k \rvert}=g^\prime(k+)$
$\displaystyle\lim_{x\to k-}-\frac {g(x)-g(k)}{\lvert x-k \rvert}=g^\prime(k-)$
$g^\prime(k+)$와 $-g^\prime(k-)$이 같다는 것은 $g^\prime(k)$가 절댓값으로 인해 부호가 반대로 되는 첨점이거나 부호의 영향을 받지 않는 0일 것이다.
2. 상황을 대충 이해했으니 임의의 상황에 적용시켜서 이해도를 더욱 높여보자.

임의의 4차 함수 곡선이다. 점선은 변하는 $y=t$를 표현한 것으로, 해당 지점에서 접었을 때 $h(t)$의 개수를 표현한 것이다.
이렇게 이해해 보면 결국 극점에서 $h(t)$의 불연속점이 발생한 다는 사실을 알 수 있고, 앞으로 불연속점에 집중해 문제를 풀어나가면 될 것이라는 전략을 수립할 수 있다.
3. 개형의 후보를 정해보자.

(가) 조건을 먼저 보았지만, 할 것이 너무 없어 (나) 조건으로 넘어왔다.
$h(t)$가 불연속 점이 2개"만" 있다는 제한 조건에 집중해 풀이를 진행해 보자. 4차 함수의 개형은 위와 같이 크게 4개로 분류할 수 있다.
첫 번째의 경우) 극값이 하나이므로 탈락
두 번째의 경우) 극값은 하나이지만, 3중 근인 지점에서 $h(t)$의 불연속점이 생기므로 합격
세 번째의 경우) 극값이 세 개이므로 탈락
네 번째의 경우) 극값이 두 개이므로 합격
합격한 두 개형의 극값은 위에서부터 $4$, $-60$인 것을 알 수 있다.
4. 후보 결정 완료. 남은 조건으로 정답 개형을 결정해 보자.

(가) 조건의 $\displaystyle\lim_{t\to 4+} h(t)=5$을 사용하면,
첫 번째 개형과 두 번째 개형 모두 해당하지 않는다. 자동적으로 세 번째 개형 합격
5. 개형 결정 완료. $f(x)$를 구해보자.
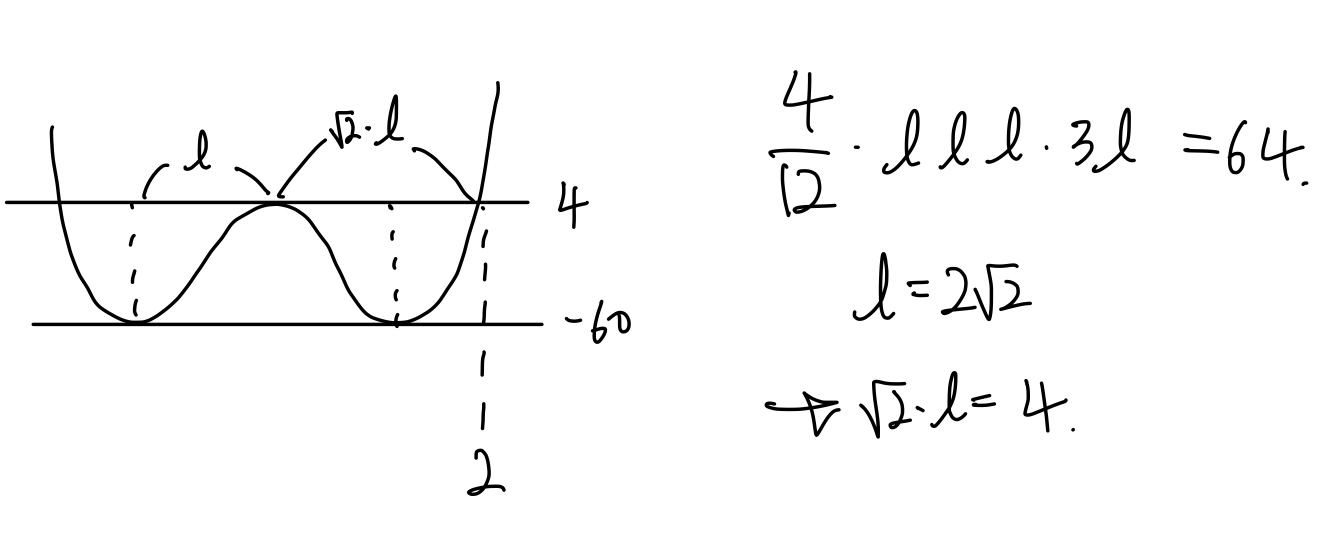
우선 좌우대칭 4차 함수의 극값의 차가 $64$이므로 극점의 $x$좌표는 3차 함수의 넓이 공식을 이용해 구할 수 있다.
$\displaystyle \frac4 {12}\cdot l^3 \cdot 3l=64$
$l=2\sqrt2$
4차 함수의 비율관계($1:\sqrt2$) 에 의해 $y=4$와 접하는 점 사이의 거리는 $4$라는 것을 구할 수 있다.
6. 남은 것은 계산과 정답 구하기.

$f(x)=(x-2)(x+2)^2(x+6)+4$이다.
$\begin {align} f(4)&=2\cdot 6^2\cdot10+4\\
&=724\end {align}$
$h(4)=5$
$\begin {align} f(4)+h(4)&=724+5\\
&=729\end {align}$
$\therefore 729$
아마 처음에 문제 상황 이해만 잘 했다면 나머지를 따라오는 것은 문제 없었을 것이다. 혹시 이해가 잘 되지 않는 부분이 있다면 댓글로 편하게 질문 바라고 모두 수능을 보는 그날까지 파이팅이다.
이 문제를 나쁘지 않게 따라와 해결했다면 2023학년도 수능 공통 22번을 풀어보자. 상황 이해를 중심으로 문제를 풀면 된다. 아래에 문제 파일을 올려두겠다.
2023.04.30 - [모의고사·수능/수학 2023학년도] - 2023학년도 11월 (대수능) 수학 공통 22번 해설, 문제, 정답, 풀이 [231122m]
2023학년도 11월 (대수능) 수학 공통 22번 해설, 문제, 정답, 풀이 [231122m]
필자의 부족한 평가 질린다. 하지만 질리도록 풀어도 새롭다. (뭐 이런 모순적인) 이전에 기출문제에서 자주 본 형식의 문제이다. (가) 조건에 주어진 식을 이항하고 나누어 기울기로 해석하는,
seook.tistory.com
학습에 도움이 되었으면 하고, 앞으로 검색할 때 여기에서 우선적으로 찾으면 편하게끔 하려고 한다. 혹시 풀이가 필요한 수학문제, 국어문제, 물리문제가 있다면 무슨 모의고사 몇 번 문제인지 아래 폼으로 알려주면 우선적으로 추가하겠다.
파일을 포함한 질문은 여기로 >> https://forms.gle/mMjHoqgRuY1dUtyy9
문제 검색 하는 법
문제 검색 하는 법 : [학년도/시행월/문제번호/과목명]
과목명 : [m - 수학 1ᐧ수학 2ᐧ미적분, k - 독서ᐧ문학ᐧ언어와 매체, p - 물리학 1]
ex) 24학년도 6월 모의고사 미적분 30번 풀이의 경우 "240630m"(으)로 검색
(2023년 시행 교육청 모의고사의 경우에도 [24xxxxx]로 검색)
혹시 오류가 있다면 언제든 지적 부탁드립니다! 감사합니다!
'모의고사·수능 > 수학 2024학년도' 카테고리의 다른 글
| 2024학년도(2023년 시행) 6월 수학 공통 22번 (오답률 1위) 엄청 쉬운 풀이, 문제, 정답, 해설, 정답률 [240622m] (0) | 2023.06.25 |
|---|---|
| 2024학년도(2023년 시행) 6월 모의고사 공통 12번 해설, 문제, 정답, 풀이 [240612m] (0) | 2023.06.25 |
| 2024학년도(2023년 시행) 6월 모의고사 공통 13번 해설, 문제, 정답, 풀이 [240613m] (0) | 2023.06.24 |
| 2024학년도(2023년 시행) 4월(5월) 모의고사 공통 15번 해설, 문제, 정답, 풀이 [240415m] (1) | 2023.05.17 |
| 2024학년도(2023년 시행) 4월(5월) 수학 미적분 29번 해설, 문제, 정답, 풀이 [240429m] (0) | 2023.05.10 |




