JS
2024학년도 대학수학능력시험 공통영역 22번 해설, 문제, 정답, 풀이 [241122m] 본문
문제
최고차항의 계수가 1인 삼차함수 f(x)가 다음 조건을 만족시킨다.
조건) 함수 f(x)에 대하여, f(k-1)f(k+1)<0 을 만족시키는 정수 k는 존재하지 않는다.
f'(-1/4)=-1/4, f'(1/4)<0일 때, f(8)의 값을 구하시오.

정답
주관식 : 483
해설
모든 정수 k에 대하여, $f(k-1)f(k+1)<0$을 만족시키는 정수 $k$는 존재하지 않는다라는 발문을 다시 생각해보면 아래와 같다.
모든 정수 k에 대하여, $f(k-1)f(k+1)\geq{0}$을 만족시킨다.
그러니 우리는 이제부터 양수*양수, 음수*음수와 같이 곱한 값이 0보다 큰 부분이 아니라, f(x)와 x축과의 교점 주변을 중심으로 관찰해야한다. 교점 주변에서 f(k-1)f(k+1)이 음수*양수가 되는 일을 방지해야한다. 그러기 위해서는, 함숫값이 음수가 나올 때는 반대쪽 값을 음수나 0으로 맞추어 주어야 한다.

이런 상황을 생각해보면 아래와 같은 경우를 생각할 수 있다. (필자가 생각한 순서이다)
이중, 정답인 개형은 iii)개형으로, 평소에 답이 나오던 형태와 달라 아마 현장에서는 어렵지 않았을까 싶다.

iii) 가정으로 바로 들어가보자. $\displaystyle{f'}\left(-\frac14\right)=-\frac14,{f'}\left(\frac14\right)<0$라는 조건을 이용해 계산 양을 줄일 수 있다.
$\displaystyle{f'}\left(-\frac14\right)=-\frac14$인 x좌표의 후보는 아래 그림과 같이 1번과 2번으로 볼 수 있다.

만약 2번위치가 $x=-\frac14$라고 가정하면, $\gamma=0$인데, $\displaystyle{f'}\left(\frac14\right)<0$라는 조건에서 모순이다.
따라서, $\displaystyle{f'}\left(-\frac14\right)=-\frac14$를 만족시키는 x좌표는 1번이다.

1번 좌표가 $-\frac14$이고, $\beta=0$, $\gamma=1$이다. 그럼 아래와 같이 함수에 대한 식을 세울 수 있다.
$$f(x)=x(x-1)(x-\alpha)$$

$\displaystyle{f'}\left(-\frac14\right)=-\frac14$라는 조건을 이용해 $\alpha$를 구하면, $\displaystyle\alpha=-\frac58$이다.
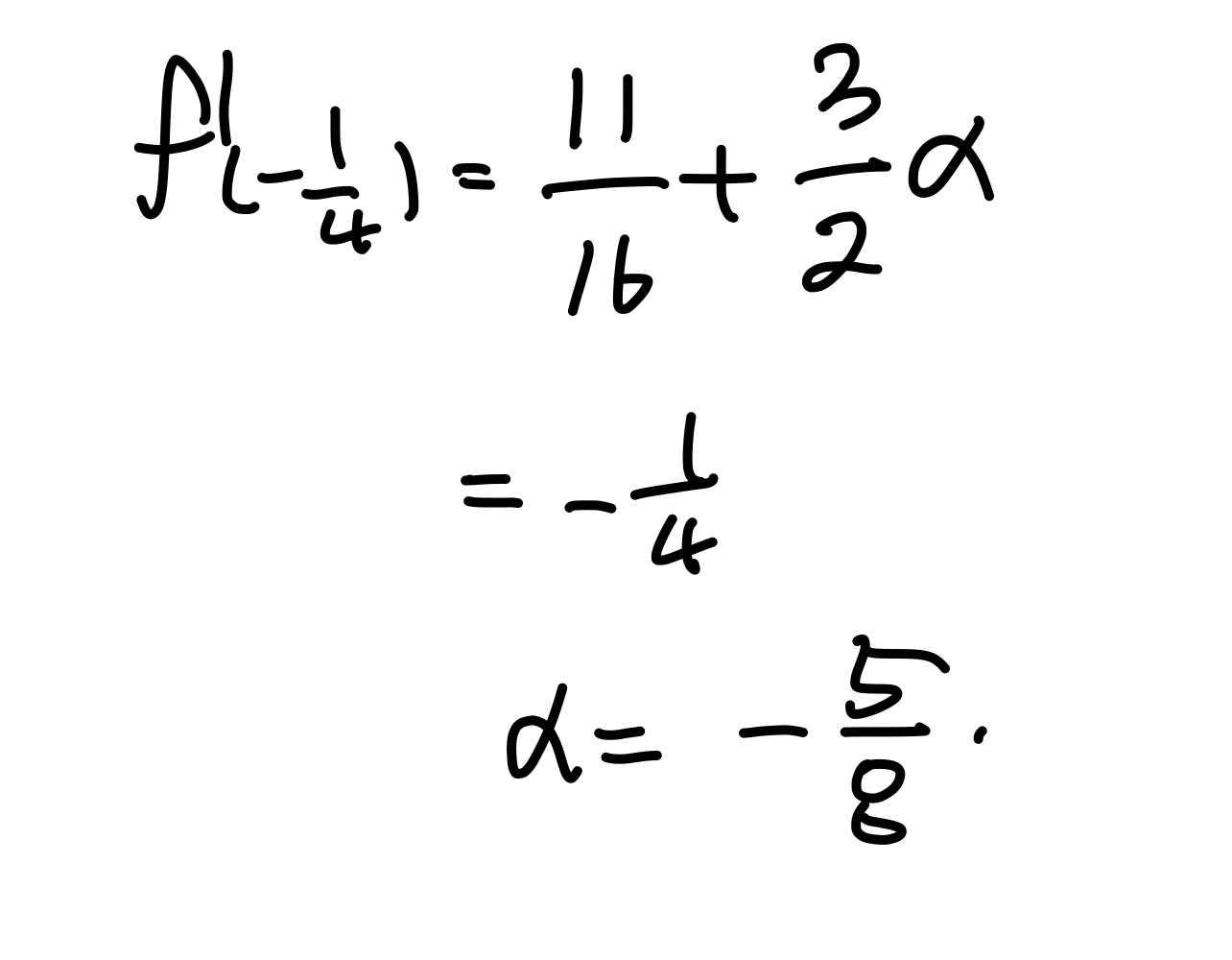
$$\displaystyle f(x)=\frac18x(x-1)(8x+5)$$
$$\displaystyle f(8)=8\times7\times\frac{69}8=483$$
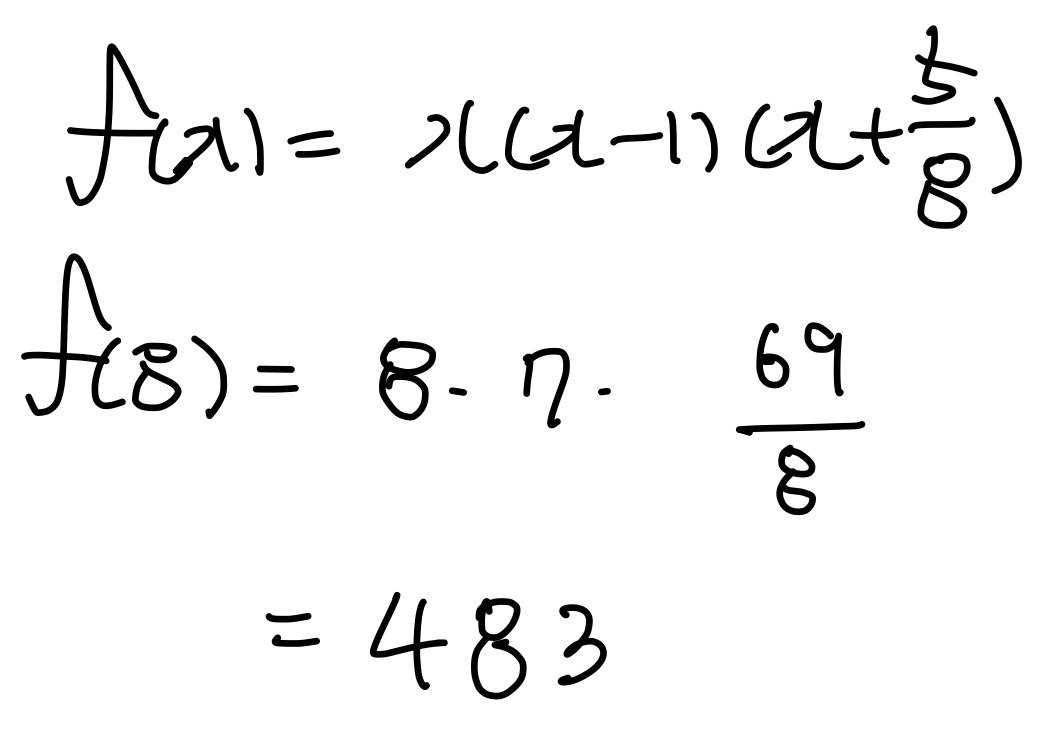
문제 검색 하는 법
문제 검색 하는 법 : [학년도/시행월/문제번호/과목명]
과목명 : [m - 수학 1ᐧ수학 2ᐧ미적분, k - 독서ᐧ문학ᐧ언어와 매체, p - 물리학 1]
ex) 24학년도 6월 모의고사 미적분 30번 풀이의 경우 "240630m"(으)로 검색
혹시 오류가 있다면 언제든 지적 부탁드립니다! 감사합니다!
'모의고사·수능 > 수학 2024학년도' 카테고리의 다른 글
| 2024학년도 대학수학능력시험 미적분 30번 해설, 문제, 정답, 풀이 [241130m] (0) | 2023.11.20 |
|---|---|
| 2024학년도 대학수학능력시험 공통영역 20번 해설, 문제, 정답, 풀이 [241120m] (0) | 2023.11.18 |
| 2024학년도 9월 모의고사 미적분 30번 해설, 문제, 정답, 풀이 [240930m] (5) | 2023.09.07 |
| 2024학년도(2023년 시행) 4월(5월) 모의고사 공통 15번 해설, 문제, 정답, 풀이 [240415m] (0) | 2023.06.27 |
| 2024학년도 6월 미적분 29번 엄청 쉬운 풀이 / 틀렸으면 들어와서 확인하기! [240622m] (1) | 2023.06.27 |




