JS
2023학년도 11월 (대수능) 수학 공통 22번 해설, 문제, 정답, 풀이 [231122m] 본문
https://seook.tistory.com/entry/241122m
2023년 11월 16일에 시행한 대학수학능력시험 수학 공통 22번 해설은 아래 링크로
2024학년도 대학수학능력시험 공통영역 22번 해설, 문제, 정답, 풀이 [241122m]
문제 최고차항의 계수가 1인 삼차함수 f(x)가 다음 조건을 만족시킨다. 조건) 함수 f(x)에 대하여, f(k-1)f(k+1)
seook.tistory.com
필자의 부족한 평가
질린다. 하지만 질리도록 풀어도 새롭다. (뭐 이런 모순적인)
이전에 기출문제에서 자주 본 형식의 문제이다. (가) 조건에 주어진 식을 이항하고 나누어 기울기로 해석하는, 과거 기출문제에서 (가)조건을 해석하고 사용하는 부분이 똑같이 출제되었다. 하지만, 출제자의 킥이 있다면, $f^\prime(g(x))$에서 $g(x)$를 해석하는 부분이 관건이었던 것 같다. 필자도 현장에서 이 문제를 맞닥뜨렸을 때 부끄럽게도 해당 부분을 적절하게 해석하지 못해 풀지 못했던 기억이 난다.
분명 6월 9월 모의고사에서는 백분위 99 100이 나오는 사람도 수능 시험장에 들어가 시험 보기 전까지는 모르는 법. 이 글을 보고 수능을 준비하는 모두, 정말로 철저히 준비하자. 문제를 풀 때 일반 풀이 원칙을 세우자. 감정에 휩싸였을 때 패닉된 상황을 헤쳐나가기 위해서는 기계처럼 할 수 있는 도구가 필요하다. (물론 그냥 엄청 잘하면 이런 것도 필요 없음)
이 문제는 확실히 기출문제에서 근거해 출제된 문제로, 평가원에서 기출 문제 학습을 중요시 하라는 신호로 보인다.
문제


만약 아래 글이 위 사진처럼 자연스럽게 보이지 않는다면? >> https://seook.tistory.com/19
최고차항의 계수가 $1$인 삼차함수 $f(x)$와 실수 전체의 집합에서 연속인 함수 $g(x)$가 다음 조건을 만족시킬 때, $f(4)$의 값을 구하시오.
(가) 모든 실수 $x$에 대하여
$f(x)=f(1)+(x-1) f^\prime(g(x))$이다.
(나) 함수 $g(x)$의 최솟값은 $\displaystyle\frac52$이다.
(다) $\displaystyle f(0)=-3,\,f(g(1))=6$
정답
( 주관식 ) $13$
해설

$f(x)=f(1)+(x-1) f^\prime(g(x))$, $\quad f(x)$를 앞으로 이항 하면,
$f(x)-f(1)=(x-1) f^\prime(g(x))$, $\quad (x\neq1)$을 가정하고 나누어주면,
$\displaystyle \frac {f(x)-f(1)}{x-1}=f^\prime(g(x)),\quad(\text 단, x\neq1$) 을 구할 수 있다.
위 식을 대수적으로 판단하기에는 단서가 부족해 보인다. $g(x)$가 미분가능한 다항함수라고 주어지지 않았을뿐더러, 계산하기에는 꼴이 너무 복잡하기 때문이다. 따라서 기하적으로 해석을 하려 한다.
$f^\prime(g(x))$는 $(x, f(x))\text와\,(1, f(1))$을 이은 기울기에 해당하는 접점이라 해석할 수 있다.
이를 그림으로 이해하면, 다음과 같이 전개된다.





1. $(1, f(1))$에 해당하는 한 점을 임의로 잡는다. (처음 왼쪽 분홍색 점)
2. $(x, f(x))$에 해당하는 한 점을 임의로 잡는다. $(x\neq1)$ (두번째 오른쪽 분홍색 점)
3. 두 점 사이를 잇는 선분을 그리고, 해당 선분의 기울기를 갖고 $f(x)$와 접하는 직선을 두 개 그린다.
4. 두 접점 중 한 점이 $g(x)$의 치역에 해당한다.
위에서 정리한 내용을 바탕으로, $x$를 $1$로 극한을 보내보자.
$\begin {align}\displaystyle \lim_{x\to1} f^\prime(g(x))&=\lim_{x\to1}\frac {f(x)-f(1)}{x-1}\\
&=f^\prime(1)\end {align}$
$g(1)$이 될 수 있는 점의 후보는 두 개가 있는데, 뒤에 있는 (나) 조건$\displaystyle\left(g(x)\geq\frac52\right)$에 의해 오른쪽 점으로 확정된다.
또, (나) 조건을 계속 사용하기 위해 특수한 경우까지 g(x)의 치역을 구하다 보면, $(1, f(1))$과 $f(x)$가 접할 때 $g(x)$가 최솟값을 갖는 것을 알 수 있다. 따라서 해당 점의 $x$좌표는 $\displaystyle\frac52$이다. (아래 그림 참고)


이게 어려운 것은 끝났다. 남은 건 계산.
삼차함수의 비율 관계에 의해 다른 점들의 $x$좌표를 마저 구할 수 있고, $g(1)=3$이란 것도 구할 수 있다. 따라서 (다) 조건에 의해 $f(3)=6$이다.
또, 두 접하는 점 간의 거리가 $1$임을 알 수 있으므로 두 직선의 연직 거리를 구할 수 있다. $x^3$의 계수가 $1$이므로, $\displaystyle \frac36\cdot1^3=\frac12$이다. 아래 직선이 지나는 점의 좌표는 $\displaystyle\left(3,\frac {11}2\right)$이다.
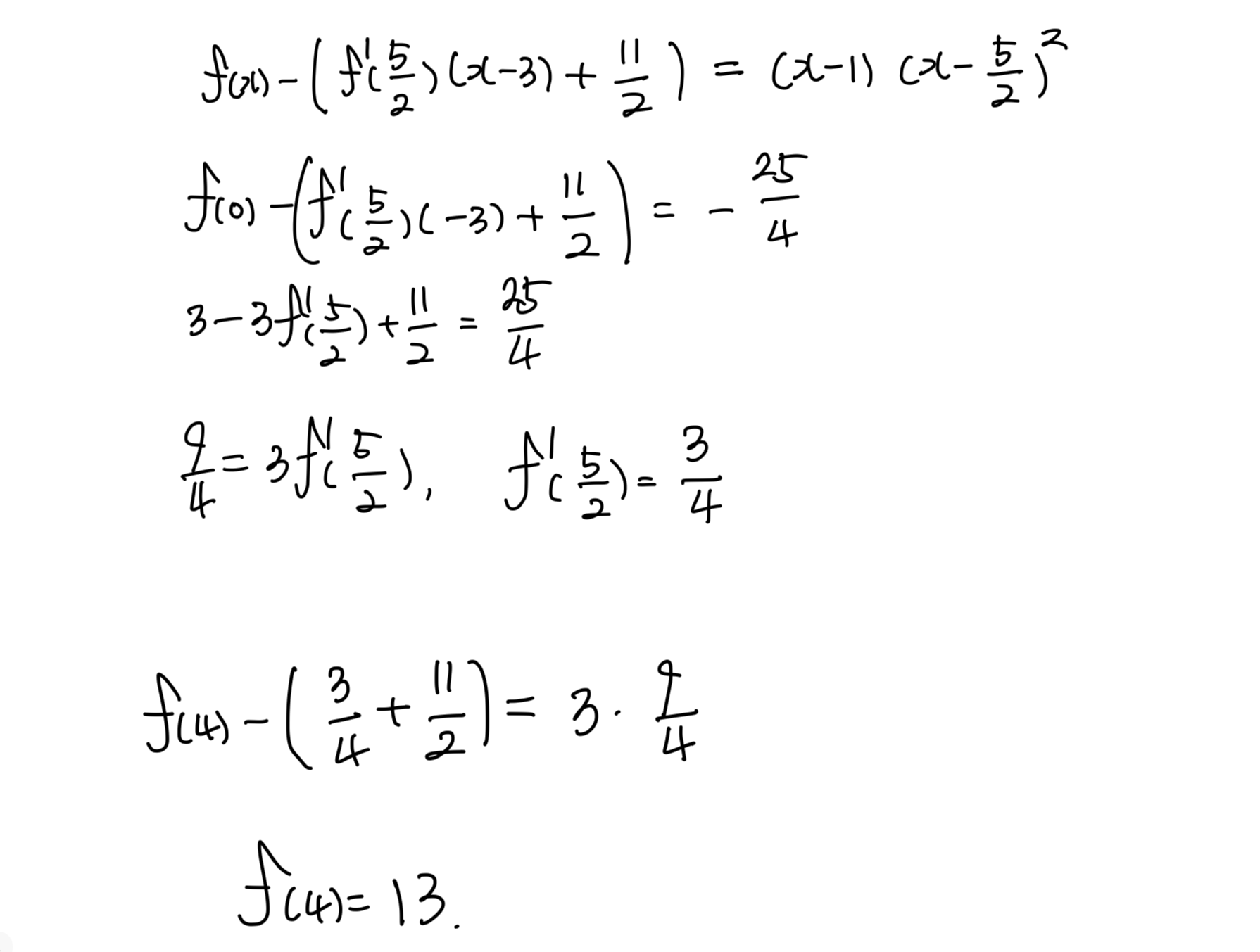
따라서, $\displaystyle f(x)-\left(f\prime\left(\frac52\right)(x-3)+\frac {11}2\right)=(x-1)\left(x-\frac52\right)^2$이고,
$f(0)=3$을 이용해 $\displaystyle f^\prime\left(\frac52\right)$를 구할 수 있다.
$\displaystyle f^\prime\left(\frac52\right)=\frac34$
다시 $x$에 $4$를 대입해 $f(4)$를 구하면 다음과 같다 (계산 생략, 사진 참고)
$\displaystyle\therefore f(4)=13$
정말로 두번째 $f^\prime(g(x))$ 해석만 잘 했으면 쉽게 풀었을 문제이다. 실제 예시를 들며 상황을 이해할 수 있는 능력을 키워야 함을 알 수 있는 계기로 삼을 수 있으면 좋겠다.
학습에 도움이 되었으면 하고, 앞으로 검색할 때 여기에서 우선적으로 찾으면 편하게끔 하려고 한다. 혹시 풀이가 필요한 수학문제, 국어문제, 물리문제가 있다면 무슨 모의고사 몇 번 문제인지 아래 폼으로 알려주면 우선적으로 추가하겠다.
파일을 포함한 질문은 여기로 >> https://forms.gle/mMjHoqgRuY1dUtyy9
문제 검색 하는 법
문제 검색 하는 법 : [학년도/시행월/문제번호/과목명]
과목명 : [m - 수학 1ᐧ수학 2ᐧ미적분, k - 독서ᐧ문학ᐧ언어와 매체, p - 물리학 1]
ex) 24학년도 6월 모의고사 미적분 30번 풀이의 경우 "240630m"(으)로 검색
혹시 오류가 있다면 언제든 지적 부탁드립니다! 감사합니다!
'모의고사·수능 > 수학 2024학년도 이전' 카테고리의 다른 글
| 2022학년도(2021년 시행) 11월(대수능) 미적분 29번 삼도극 풀이, 식 근사 풀이, 정답, 문제 [221129m] (0) | 2023.06.27 |
|---|---|
| 2023학년도 11월 (대수능) 미적분 30번 해설, 문제, 정답, 풀이, n축[231130m] (0) | 2023.04.28 |
| 2023학년도 11월 (대수능) 미적분 29번 해설, 문제, 정답, 풀이 [231129m] (0) | 2023.04.28 |
| 2023학년도 9월 미적분 28번 삼도극 풀이, 식 근사 풀이, 정답, 문제 [230928m] (0) | 2023.04.27 |
| 2023학년도 11월(대수능) 미적분 28번 풀이, 식 근사, 도형 근사 풀이, 정답, 문제 [231128m] (0) | 2023.04.27 |




